| General Discussion Undecided where to post - do it here. |
| Reply to Thread New Thread |
|
|
#1 |
|
|
Hey everyone,
I am sort of struggling with a mathematical problem.  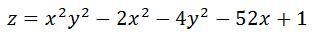 Here's the deal, I need to show that that equation has 3 stationary points (and say what their positions are) and if they are a maximum, minimum, or a saddle point. Can anyone show me the solution to this? (A step by step solution to solving it would do me wonders too). Thanks! Edit: used my gfs laptop to post and its behaving a bit strange as it didnt post the image for some reason so im on mine now. (Have another post about it somewhere here - IE doesnt load youtube vids or cant login to facebook or open hotmail... I used Firefox to post this from hers and its the 1st time ive had trouble with it...) |
|
|
|
|
#2 |
|
|
I'm assuming because you are as far as multivariate calculus that you know how to differentiate. Partial differentiation means you assume the variable you aren't differentiating with respect to is a contstant, so differentitating 5y with respect to x equals 0, but 5yx would give 5y.
Since I can't be bothered to a) set this up in an equation editor or b) give you an answer for your homework, I'll define dxf to be the first partial with respect to x, dyf wrt to y hence dxxf is the second partial wrt x etc. You therefore need to find: dxf dxxf dyf dyyf dxyf (=dyxf if you want to check you have done things correctly) Stationary points are found in the usual way setting first partials to zero and solving. To find their properties, you need to test the sign and magnitude of the multiple of dxxf and dyyf against the square of dxyf. Your notes should explain what the outcomes of the test are (they may define a matrix M so that the sign of M is your indicator as the determinant will be dxxfdyyf - dxyf^2). |
|
|
|
|
#4 |
|
|
|
|
|
|
|
#5 |
|
|
Yeah, thanks everyone, I managed to do it! Proved to be quite easy once I understood the basics!
Now, im sort of stuck on another Question... if youre willing to help ^^ Im not going to go through the whole thing coz I cant be bothered to type it all up (and use the eq editor), so I will just show you where exactly I am stuck. Heres the deal: 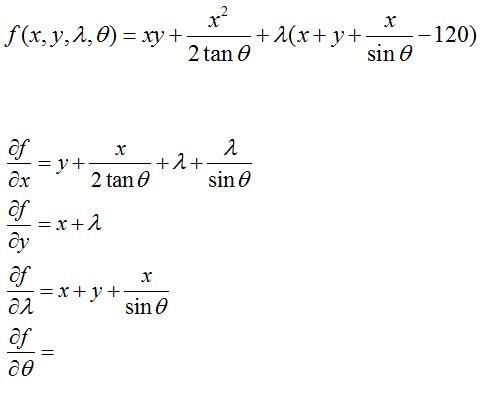 So yeah, I am finding it really tricky to differentiate with respect to theta... Anyone help? Thanks again for the support! |
|
|
|
|
#6 |
|
|
Yeah, thanks everyone, I managed to do it! Proved to be quite easy once I understood the basics! x/(2* tan(theta)) should be x/(tan(theta)) dF(lamda) is wrong too!!! Should be: x + y + x/(sin(theta)) - 120 dF(theta) is not too bad. dF(theta) = x^2/2 * dF(theta) [1/tan(theta)] + lamda * x dF(theta) [1/sin(theta)] The rest is up to you!!! HINT: all you need to find is to find out what is the derivative of 1/tan(x) and 1/sin(x), and there you go. |
|
|
|
|
#7 |
|
|
dFx is wrong. Thanks! |
|
|
|
|
#8 |
|
|
|
|
|
|
|
#9 |
|
|
|
|
|
|
|
#10 |
|
|
|
|
|
|
|
#11 |
|
|
The derivative of cot(theta) is -csc^2(theta). Look up what "cotangent", "secant" and "cosecant" really are. The very definition of those operators is the answer to your question. Some advice, my friend, take it or leave it: You will never succeed in a Math course if you do not know the fundamentals. Getting the answer to this question handed to you will NOT help you one bit. Good luck! |
|
|
|
|
#12 |
|
|
I would love to help, but what you are asking is a REALLY fundamental question. |
|
|
| Reply to Thread New Thread |
«
Previous Thread
|
Next Thread
»
| Currently Active Users Viewing This Thread: 1 (0 members and 1 guests) | |
|
|






 Linear Mode
Linear Mode


