[ballingham]

Puts, uncovered puts, married puts, uncovered index puts

All just different varieties of the olympic event.

Calls, write cover calls, index calls, uncovered equity This is referring to call girls, of course, i.e. prostitution.

Spreads (vertical, calendar, diagonal) Prostitution, again.

Straddles More prostitution. Hm, I'm noticing a pattern...

• Strangles
• Collars
• Greeks
• Butterfly, iron butterfly
• Condor, iron condor Yep. Prostitution.

Honestly, the whole shot put thing seems very out of place. If this were a "one of these things is not like the other" question you'd be set.

[imnaone]

ask kh, he'll be happy to do your homework for you!

Bullshit. That pompous ass would ask her to explain what she thinks each is and then tell her to re-read her sources.

Give me a minute. I'll do it...

[Vegeinvalge]

Please write a good explanation (step by step guideline for "dummies") for the attached question.

With respect to options on stock market, explain in detail, with one or two clear examples of the following terms:

• Puts, uncovered puts, married puts, uncovered index puts
• Calls, write cover calls, index calls, uncovered equity
• Spreads (vertical, calendar, diagonal)
• Straddles
• Strangles
• Collars
• Greeks
• Butterfly, iron butterfly
• Condor, iron condor
can anyone explain this to me? it's the difference between an A and a B+, and I really would like to do this, but google isn't helping me as much as I'd like...


so far I have

"A "put"/ "put option" is an option to sell an item at a preset price at some time in the future, but not an obligation.
For example, A stock is at $5.45 and someone wants a put. They make an agreement with the current owner of the stock to sell it for this price in the future. It is just the option to sell it, not the obligation to."

I don't know how much you know and certain things omitted from your definition of a put make me concerned you do not have a full picture so I will be very in depth and assume little prior knowledge:

To understand options, you have to first understand the other derivatives: futures and forwards. Forwards are obligations to buy or sell an underlying asset at an agreed upon price (the delivery price) in the future. This is contrasted with a spot transaction which would be a purchase at the present time for the present (or spot) price.

While speculative reasons for forward contracts are obvious, they were developed as hedges for risk. For example, a farmer can not know what price his wheat will fetch on the market after harvest months away; while a miller also will not know how much the wheat he purchases will cost. By entering into a forward contract, both are able to lock in a price, which reduces their risk exposures. If in the future, the spot price of wheat is different from the delivery price on the futures contract, that difference is the forward premium or discount (think of it as a profit/loss for the purchasing party).

Forward contracts (as well as all other derivatives) are two-party transactions; there is a buyer and a seller (or writer). These terms are only for convenience; forward and futures contracts do not have a cost to enter. The party who agrees to buy the underlying asset at the agreed-upon price (the miller in the above example) is said to assume a 'long' position; the party agreeing to sell the underlying asset assumes a 'short' position.

To understand how the spot price relates to the delivery price for both long and short positions, here's two charts with K representing the strike price: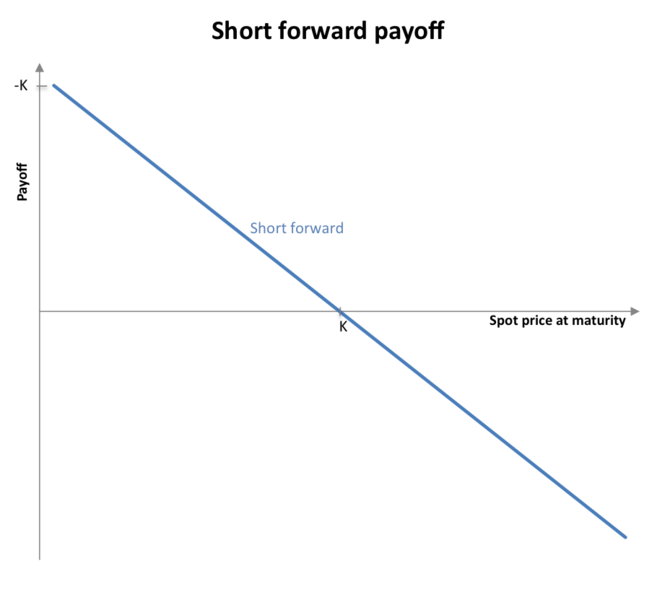





As you can see, the relationship is simple for forward contracts. In a long position, if the spot price of the asset equals the strike price at time of expiration, no profit/loss is made, but price risk has been mitigated. If the spot price is greater than the strike price, a profit is made in the long position, while a loss is suffered in the short position.

Futures are similar to forward contracts but are standardized contracts with an exchange. The Chicago Board of Trade was the world's first and premier futures exchange. To minimize credit risk, the exchange requires traders to post margin; to minimize counter-party risk to the traders (the risk that the other party of the futures contract will not fulfill their obligation), the exchange guarantees trades through a clearing house, which effectively becomes the buyer/seller on every futures transaction. I'm not going to get into margin requirements. Other than these differences, futures contracts are just like forwards contracts and have the same payout schedules, as represented by those charts above.

Unlike futures and forwards, options are not obligations but contain the right to buy or sell an underlying asset at the agreed upon strike price. Because of this difference, options are priced, unlike the other types of derivatives. This price of the option derives from the difference between the strike price and the spot price of the underlying asset plus a premium based on the time remaining til expiration. The premium is collected by the seller (or writer) of the option.

For options, terms like 'long' and 'short' do not mean precisely the same thing as for forwards and futures. As you will remember, someone assumes a long position in a futures contract by agreeing to buy the underlying asset. For options, one assumes a long position by purchasing the option, whether it is a call or put; that is, whether the party is purchasing the right to buy or sell the underlying asset. The 'short' position in an options contract is taken by the writer of the option; the writer promises to fulfill the options contract if the buyer exercises the option.

Calls are options to buy the underlying asset at the strike price; puts are options to sell the underlying asset at the strike price.

Here are the payout schedules. If they are not understandable, I can explain them:

This is a long put position. The buyer of this put has the right to sell the underlying security at the strike price:



This is a long call position. The buyer of this call has the right to buy the underlying security at the strike price:



As you can see from both payouts, options mitigate risk because if the spot price varies from the strike price such that the possessor of the option will incur a loss, the option will not be exercised.

Note also the effect of the premium on the payout. Because the option contract cost money to enter, that cost diminishes the potential profit. It is also a sunk cost in the transaction that was incurred regardless of whether or not the option is exercised.

Being long a call, therefore, means that, if the spot price is less than the strike price at time of expiration, the option will not be exercised and the premium will be the only loss incurred. Losses on the downside are minimal. If the spot price is greater than the strike price plus the cost of the premium, a profit is generated for the long position. This profit is potentially unlimited.

The payouts for the writer of the option are different:
Short Call:


Short Put:


As you can see, writing options involves substantial risk. Losses are potentially unlimited while profits are limited to the premium.

[ExelePlavisseu]

You sure this site isn't sufficient to explain all the strategies?

http://www.theoptionsguide.com/optio...trategies.aspx

It goes pretty in depth about all of them I think and is easy to understand.


And the greeks are the oddball on your list. They are measures of risk sensitivity. That site also has in depth and easy to understand explanations for the greeks.

[SergeyLisin]

Honestly, the whole shot put thing seems very out of place. If this were a "one of these things is not like the other" question you'd be set.

Its more akin to porn what with the money shot (put) and all. Long puts landing overhead and short puts on clothing.

[SergZHy67]

Oh and one thing I forgot to mention... Out-of-the-money refers to an option with no intrinsic value. For example, a put is out of the money if the spot price is greater than the strike price. At-the-money refers to an option with a strike price that is equal to the spot price.

[st01en_lox]

Why is she taking a class on derivatives anyway? I thought she was an engineering student.

[Nikitka]

Not just at that moment, and especially if you're on the receiving end

[dwestemesse]

I took this class last term. This is just an extra credit assignment for my IME 251 class.
(Introductory course on economic and financial analysis to assist engineering managers in making fiscally sound decisions. Topics include financial measures such as Return On Investment, Break-even Analysis, Replacement Analysis, Depreciation and Taxes, and Multiple-criteria Decision Making.)
I'm going for an industrial engineering major and this is one of the classes.

Thanks, Albie. I'll reread it all tomorrow. I'm doing a lot of packing and DDing tonight!

[Fellionas]

wait, that's DP

[herrdwq]

Which is EXACTLY what you should tell her too. You're. doing. Her. Homework.

If you want her to learn, rather than regurgitate, stop explaining.

100% of school is regurgitating.

[UFJon]

And Kuci would know.